Optimization and Control Theory Department: 2014-04-15 Nonlinear Seminar

Adam Nawrocki
Asymptotic behaviour of some 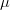$\mu$ -almost periodic functions

The function

$\begin{displaymath} f(x)=\frac{1}{2+\cos x +\cos{(x\sqrt 2)}} \end{displaymath}$ (4)
is a classical example of an unbounded and continuous 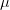$\mu$ -almost periodic function. For this function we have
$\begin{displaymath} \lim_{x\to \infty}\frac{e^{-x}}{2+\cos x +\cos{(x\sqrt 2)}}=0. \end{displaymath}$ (5)
During this lecture we will consider if changing the number 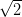$\sqrt 2$ to another irrational number may have relevant impact on the behaviour of this function. We shall construct such a number 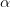$\alpha$ that the limit
$\begin{displaymath} \lim_{x\to \infty}\frac{e^{-x}}{2+\cos x +\cos{(x\alpha)}} \end{displaymath}$ (6)
will not exist.
The lecture will be preceded by a short speech by Marcin Borkowski.